Hyper-Spinoza

Si deux demi-cercles sont décrits du même centre comme A et B, l’espace compris entre les périphéries sera partout le même ; mais si deux demi-cercles sont tracés de centres différents comme C et D, l’espace compris entre les périphéries sera partout différent. La démonstration découle évidemment de la seule définition du cercle.

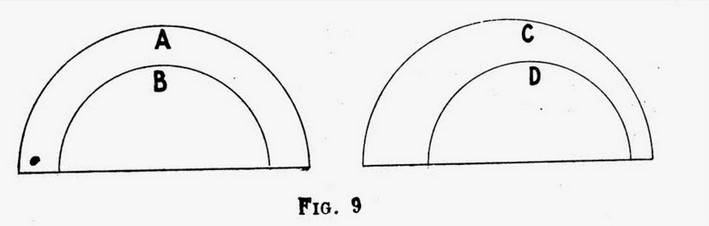
PPD - fig9